CAASPP Practice Tests: Addressing the Most Common CAASPP Mistakes
Many CAASPP practice tests aim to prepare students for the complexity of the exam, but they often fail to address the diverse skills needed to tackle each question. As a result, while students may be well-versed in content like calculating percentages, they still struggle because they lack the higher-level thinking required to understand questions, use advanced tech features, and explain their reasoning. In ELA, they might not be adequately prepared for all 4 ELA Claims that are covered on the CAASPP, including the often overlooked claim, Speaking/Listening.
In this article, we’ll explore how to target the Strategic Thinking skills crucial for improving CAASPP results.
Mathematical Strategic Thinking in CAASPP Practice Tests
Mathematical Strategic Thinking, inspired by the 8 Standards for Mathematical Practice, helps students handle the complex questions found on high-stakes assessments like the CAASPP. Students often miss questions not due to content or vocabulary gaps, but because the question design demands advanced Strategic Thinking.
There are 16 types of Strategic Thinking required on the CAASPP. Below are some of the most common and how they appear in CAASPP Math questions: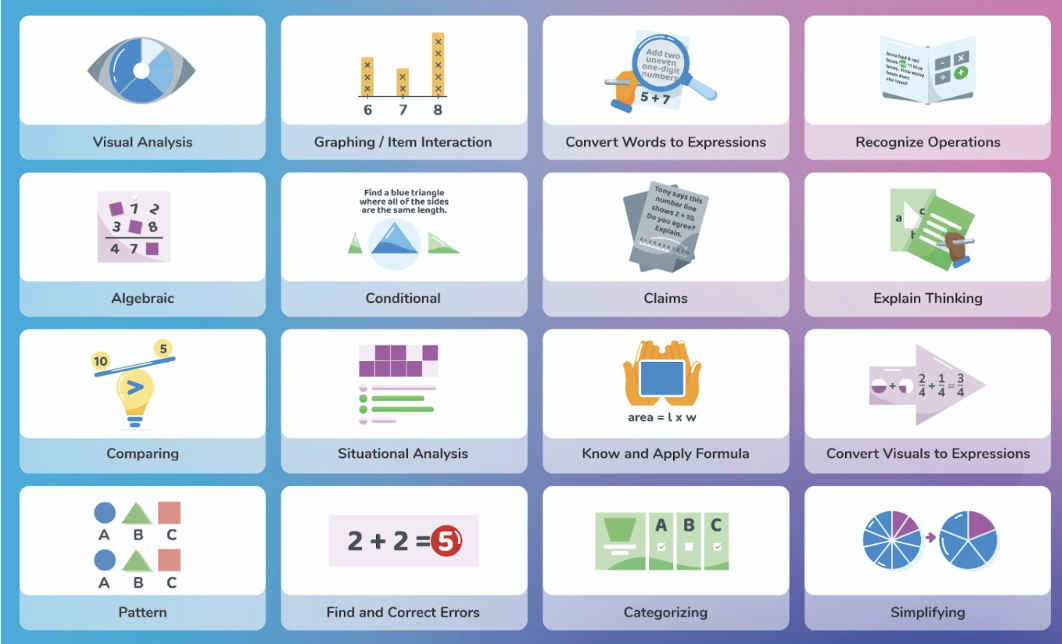
Visual Analysis and Graphing/Modeling
Visual Analysis questions ask students to interpret a graph, chart, table, or image essential to solving the problem. Graphing or item interaction may also be required, where students manipulate visuals, such as drawing a line on a graph or shading a fraction bar. Students often struggle with these questions due to unfamiliarity with the tech involved.
Claims and Explaining Thinking
In Claims questions, students assess whether a statement is correct or incorrect and provide evidence for their conclusion. This requires deeper analysis and is often paired with the need to explain steps, either in writing or by selecting the correct explanation.
Situational Analysis and Comparing
Situational Analysis requires students to evaluate multiple answers, often using a “checkbox” format. Students may mistakenly treat these as multiple-choice questions and fail to select all correct answers. Another common skill is Comparison, where students compare numbers, equations, or concepts, such as determining which number is greater or putting numbers in order.
CAASPP Practice Tests: Overlooked ELA Skills
Many students struggle with the cold read portion of the CAASPP, finding it difficult to engage with a passage independently without the usual scaffolding or class discussions. This challenge can lead to anxiety and lower performance on the test. Beyond cold reading, many curriculums don’t fully prepare students for all four CAASPP ELA claims: Reading, Writing, Speaking/Listening, and Research. These gaps can leave students underprepared for the full scope of the exam.
To address this, Classtime provides fully CAASPP-aligned cold reads that mirror the test experience, featuring authentic CAASPP question stems that are pulled directly from the Smarter Balanced Task Models. By practicing with these resources, students build the confidence and skills needed to tackle cold reads successfully. Classtime’s reading comprehensions and performance tasks are designed to ensure complete coverage of all ELA claims, including the often-overlooked Speaking/Listening component:
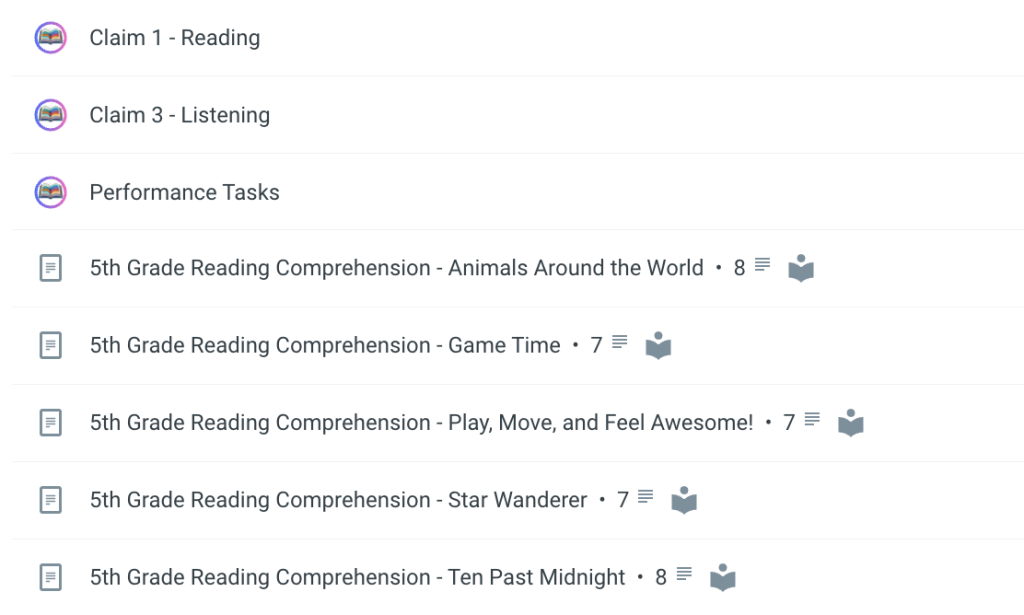
With this comprehensive approach, students gain the skills and familiarity they need to succeed in every part of the CAASPP.
Incorporating CAASPP Practice Tests into Regular Instruction
A common mistake schools make is waiting until a few months before the exam to focus on CAASPP skills through long practice tests. Instead, CAASPP skills should be woven into ongoing instruction through quick formative assessments.
For Math, one effective approach is to use Classtime’s Strategic Thinking in Math CAASPP practice tests twice a month to build familiarity with tech types and identify areas where students are struggling. Each question set includes 11 questions:
- The first is an introduction.
- The next four target math content, focusing purely on computational skills aligned with the standard. These are simpler, multiple-choice questions.
- The following four involve more advanced tech types like checkboxes, matching tables, and hot spots.
- The final two questions require students to explain their thinking or use higher levels of Strategic Thinking to solve more complex problems.
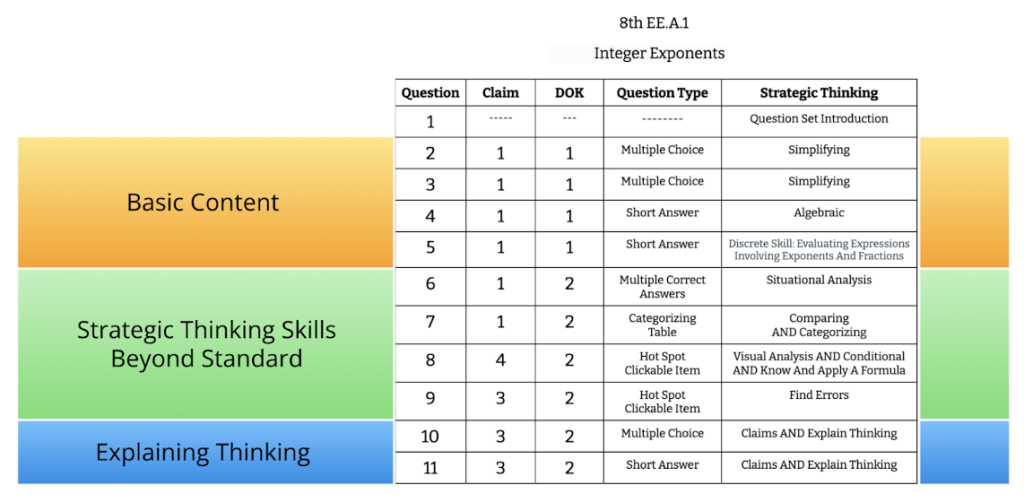
These sets can be used for quick practice in homework, quizzes, or classwork—such as a “Question of the Day” or “Exit Ticket”—allowing teachers to review live data and adjust instruction as needed. For example, if students struggle with a Categorizing question or have difficulty explaining their thinking, teachers can focus specifically on these areas.
Sample Data from CAASPP Practice Tests
Here’s an example of the data teachers receive from a question set:
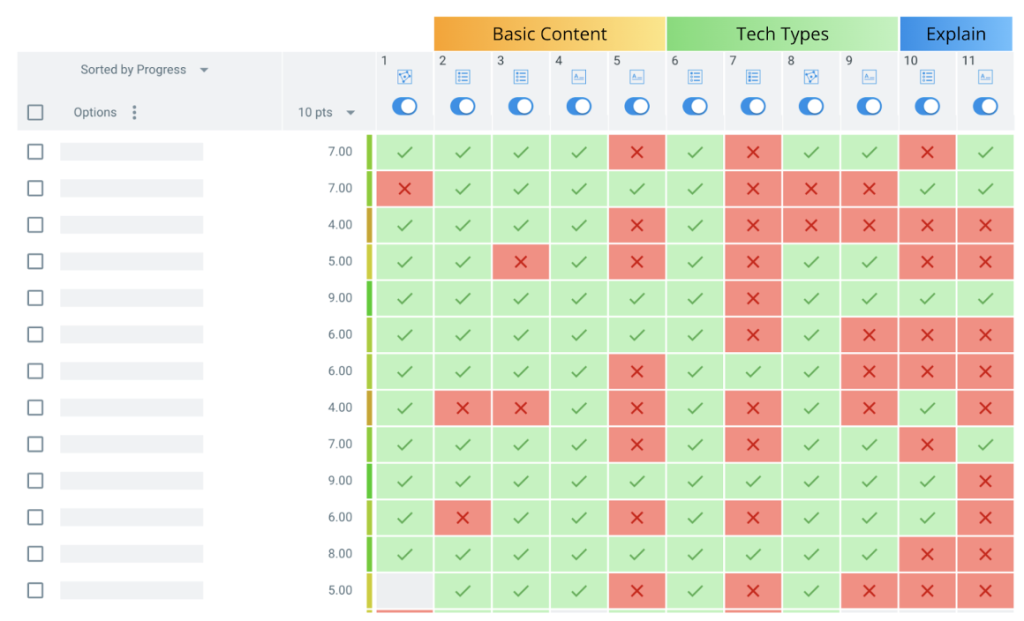
The data reveals that while students mastered the basic content, they struggled with Categorizing (Question 7) and explaining their thinking (Questions 10 and 11). With this precise feedback, teachers can target these areas in their lessons throughout the school year, better equipping their students to achieve CAASPP test score improvements.
Explore our question sets for grades 1-8 in Math below:
Below are our question sets for grades 3-8 for ELA:
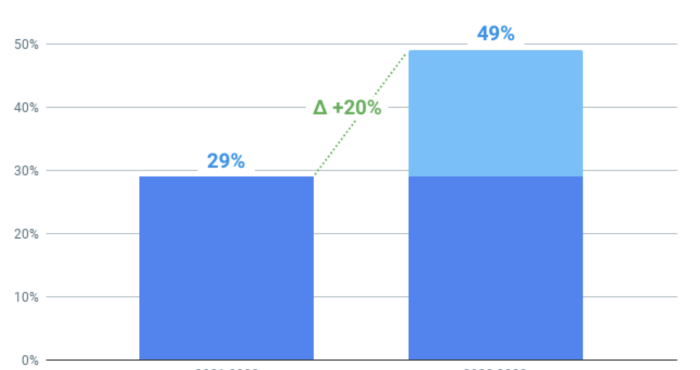
We help California districts drive significant CAASPP score improvements by focusing on Strategic Thinking in Math and ELA. Our approach is designed to move Level 2 and 3 students to proficiency by strengthening the strategic thinking skills essential to drive real, measurable gains in ELA and Math proficiency.
This has resulted in increases of Δ +20% CAASPP improvements within the first year of implementation:
We are proud to be working on Strategic Thinking in Math and ELA with forward-thinking educators at:

We are a local team that is personally committed to education in California. We’d be excited to connect for a 15-minute consultation for your school or district!


