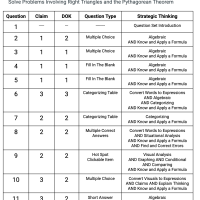
G.SRT.C.8 - Solve Problems Involving Right Triangles and the Pythagorean Theorem

From a point on level ground 120 meters from a launch pad, a drone hovering directly above the pad is at an altitude of 90 meters.

A zipline is anchored at the top of a 60-meter cliff. The landing platform is on level ground 25 meters horizontally from the base of the cliff.

A safety requirement for a new school ramp specifies that the angle θ between the ramp and level ground must satisfy sin θ = 0.5.

A survey crew measures the line-of-sight distance from a point on level ground to the top of a cliff as 120 m.

A right triangle models a ramp with the following specifications:

Select the correct method to find the missing value for each of the prompts given below.

A student tried to find the angle θ a staircase makes with the floor using rise = 1.8 m and run = 3.0 m.

There is a right triangle with vertices (0,0), (x,0), and (x,y).

Susie claims that since the triangles below are different sizes, θ must be different in each triangle.

Tyler wants to build a bike ramp.